Convex Hull

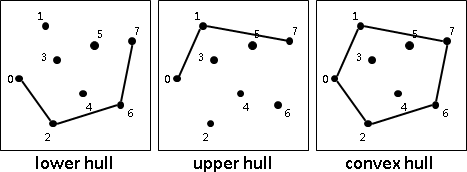
The convex hull is the smallest convex polygon containing all points in a set. Andrew’s algorithm builds it efficiently in O(n log n) time by:

1. Sorting points lexicographically (by x-coordinate, then y-coordinate)
2. Building the lower hull by traversing left-to-right, removing points that create clockwise turns
3. Building the upper hull by traversing right-to-left, similarly removing clockwise turns
4. Combining both hulls (excluding duplicate endpoints)

The key insight: at each step, we use the cross product to check if three consecutive points make a counter-clockwise turn (keep the point) or clockwise turn (remove the middle point). This ensures we only keep points on the boundary.

def cross_product(p1: tuple[int, int], p2: tuple[int, int], p3: tuple[int, int]) -> int:
    """
    Calculates the cross product (z-component) of vectors p1->p2 and p1->p3.
    > 0: p3 is left of line p1-p2 (CCW turn)
    < 0: p3 is right of line p1-p2 (CW turn)
    = 0: collinear
    """
    return (p2[0] - p1[0]) * (p3[1] - p1[1]) - (p2[1] - p1[1]) * (p3[0] - p1[0])
 
def convex_hull(points: set[tuple[int, int]]) -> list[tuple[int, int]]:
    """Returns the convex hull using Andrew's monotone chain algorithm."""
    if len(points) <= 2:
        return sorted(list(points))
 
    sorted_points = sorted(list(points))
 
    # Build lower hull
    lower_hull = []
    for p in sorted_points:
        while len(lower_hull) >= 2 and cross_product(lower_hull[-2], lower_hull[-1], p) <= 0:
            lower_hull.pop()
        lower_hull.append(p)
 
    # Build upper hull
    upper_hull = []
    for p in reversed(sorted_points):
        while len(upper_hull) >= 2 and cross_product(upper_hull[-2], upper_hull[-1], p) <= 0:
            upper_hull.pop()
        upper_hull.append(p)
 
    # Combine (excluding duplicate endpoints)
    return lower_hull[:-1] + upper_hull[:-1]
 
# Example usage
points = {(0, 0), (1, 1), (2, 2), (2, 0), (0, 2), (1, 3)}
hull = convex_hull(points)
print(f"Convex hull has {len(hull)} points:")
for p in hull:
    print(f"  {p[0]} {p[1]}")